什么是卡诺图
卡诺图,或称Karnaugh图,是一种用于简化逻辑表达式的重要工具。它通过一种图形化的方式,将逻辑表达式转化为更简洁的形式。想象一下,这就像把一个复杂的拼图变得更加清晰,让我们更容易识别出其中的结构和逻辑关系。
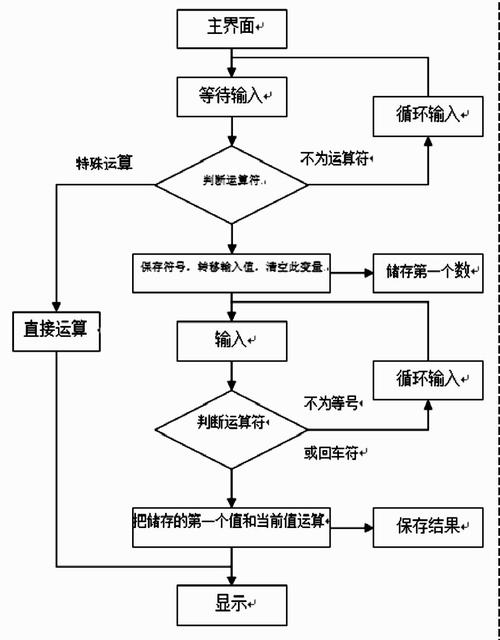
卡诺图的核心在于将表格中的所有可能组合以图形的形式排列,这样一来,我们可以通过寻找相邻的1(或0)来进行简化。不同的组合会形成不同的图形,从而帮助我们找到最优的逻辑表达式。这种图形化的表达方式让卡诺图在逻辑电路设计中颇具实用性。
卡诺图在数字电路中的应用
数字电路的设计常常需要对复杂的逻辑表达式进行简化,以减少电路的复杂性和成本。在这个过程中,卡诺图显得尤为重要。它为工程师提供了一种直观的方式来处理布尔代数,有助于实现更高效的电路设计。
不仅如此,卡诺图也广泛应用于计算机科学、电子工程等领域。在许多现实情况中,工程师们使用卡诺图来优化电路的逻辑,确保设备更高效地运行。这种应用不仅局限于大型电子设备,连小型电路的设计中也能见到卡诺图的身影。
在线化简工具的优势
在这个数字化时代,在线化简工具的出现让卡诺图的使用变得更加便捷。例如,用户可以通过浏览器随时随地访问这些工具,无需安装任何软件。这种灵活的访问方式适应了现代人的需求,节省了大量时间。
在线工具通常提供直观的界面,简化了用户输入逻辑表达式的过程。通过卡诺图化简计算器,用户不仅能快速获得结果,还能清晰地理解化简过程中的每一步。这种透明度大大增强了用户的学习体验,降低了使用门槛,让更多的人能够受益于卡诺图的强大功能。
支持的变量数量
卡诺图化简计算器的一个重要特点是它对变量数量的支持,这使得它可以处理各种复杂程度的逻辑表达式。一般来说,卡诺图主要适用于2到6个变量的逻辑函数。对于初学者来说,2到4个变量的表达式较为常见,而对于更高阶的设计,5到6个变量则能够应对一些较为复杂的应用场景。
我曾经使用过一个这样的计算器,对3个变量的逻辑表达式进行简化。这让我对化简过程有了更深的理解。每个变量的引入都会增加可能的组合,但计算器可以轻松地帮助我找到相邻的1,从而简化表达式。对于涉及更多变量的项目,在线计算器的支持显得尤为重要,它能够快速应对挑战,让我更专注于设计的其他方面。
输入格式要求
为了确保计算器能够准确处理输入内容,用户需要遵循特定的输入格式。这通常包括以特定的语法输入逻辑表达式,比如常用的与(AND)、或(OR)、非(NOT)操作符。一些在线工具还支持使用真值表形式输入,以增加灵活性。
在我使用过程中,我注意到细节非常重要。输入的格式稍有偏差,计算器可能无法正确识别。比如,输错一个括号或者误用运算符,往往会导致错误的结果或不支持的提示。在使用前花一点时间去了解这些要求,可以避免很多不必要的麻烦。
输出结果解析
卡诺图化简计算器不仅提供简化后的结果,还会详细展示每一步的化简过程。输出结果通常包括最简化的逻辑表达式,甚至可以将步骤分解为每个组合的影响。我特别喜欢这种方式,因为它能帮助我理解为何会得到这样的输出。
当我第一次看到输出结果时,发现不仅有最终表达式,还有图示化的卡诺图。这样的输出让我如同在观察一幅杰作,通过图像和文字相结合,增强了我的学习效果。每次进行优化时,我都能回顾这些细节,帮助我在电路设计中做出更明智的决策。
通过以上几个方面的功能描述,我们可以看出,卡诺图化简计算器在简化逻辑表达式时不仅高效,还为用户提供了一系列直观的支持。这使得无论是初学者还是经验丰富的工程师,都能从中获得帮助,从而更好地应用于数字电路的设计和优化中。
在线工具的访问与界面介绍
使用卡诺图化简计算器的第一步是访问在线工具网站。大多数工具都可以通过简单的搜索引擎查询找到。进入网站后,界面通常设计得简洁明了,让用户能够轻松找到所需的功能。一般来说,您会看到一个输入框,旁边可能还有一些额外的说明和输入示例。这些元素共同构成了一个易于导航的环境。
在首次访问时,我也遇到过一些不确定的地方,比如不知道该从何开始。经过几次的尝试和摸索,我逐渐适应了工具的布局。所有主要功能都在页面的一目了然的地方,这极大地减少了我的学习曲线。界面的友好设计让我可以更快地开始进行逻辑表达式的输入。
输入逻辑表达式步骤
接下来,输入逻辑表达式成为使用卡诺图化简计算器的核心步骤。通常情况下,您需要了解如何达成正确的输入格式,比如用 AND、OR、NOT 表达式来构建逻辑函数。有的工具还支持“真值表”的输入方式,这给我的使用体验带来了不少灵活性。
我在输入过程中,通过查看提供的示例,确保自己的逻辑表达式符合计算器的要求。初次尝试时,我犯过小错误,比如输入了多余的空格,这是在使用工具时需要保持警惕的地方。一旦输入完成,我会仔细检查一遍,确保没有遗漏,这样才能最大限度地提高计算准确性。
解读化简结果
输入完逻辑表达式后,点击运行按钮,我总是满怀期待地等待结果出现。计算器不仅给出最简化的表达式,还会展示化简过程中使用的卡诺图。这一过程带给我清晰的视觉效果,能够帮助我深入理解每一个步骤。
我记得第一次得到化简结果时,我发现计算器会以图示的方式呈现出所有组合的标准形式。这种可视化的输出让我更容易看懂如何从复杂的逻辑表达式中提炼出最简化的形式。同时,它还会就每一个化简步骤进行简要说明,强化了我对每个逻辑关系的理解。这种逐步解读的方式,使我在面对更复杂的问题时,能够马不停蹄地继续探索。
总而言之,卡诺图化简计算器的使用流程清晰易懂,从访问工具到输入表达式,再到解读结果,每一步都让我收获颇丰。这种便捷的使用体验使得我能够专注于更复杂的电路设计任务,有效提高了我的工作效率。
输入错误时的提示信息
在使用卡诺图化简计算器的过程中,偶尔会遭遇输入错误的情况。这种情况通常会伴随不同的提示信息。当我输入格式不符合要求时,计算器会立即给出反馈,比如显示“输入格式不正确”之类的警告。这时候,不同的工具可能会提供不同的指导,比如引导我查看输入示例或提供格式的详细说明。我发现,及时了解这些提示信息能够让我迅速纠正错误,避免再次出错。
如果输入字符串中包含了不必要的字符,比如多余的空格或错误的符号,提示信息会清楚地指出我的错误所在。例如,有一次我不小心把字母"AND"写成了"ANDD",计算器很快让我意识到了这个小错误。这些即时的反馈让我在操作过程中得以快速调整,确保最终可以得到准确的计算结果。
计算结果不准确的可能原因
有时候,即便我认真输入,计算结果可能依旧不准确。这种情况让我感到困惑,经过一段时间的探索,我总结出了一些可能的原因。首先,我意识到逻辑表达式的复杂性会影响化简的准确性。复杂的逻辑函数如果没有准确的转换成适合输入的形式,计算器很可能给出的结果也会偏离预期。
另一个原因可能是处理变量的数量。不同的卡诺图计算器可能在支持变量数量上有一定的限制。当我输入超过支持的变量数量时,结果的准确性自然就会受到影响。我逐渐学会了在使用工具之前,先熟悉一下它所能处理的表达式的范围,这样避免不必要的误差。
在线工具使用中的常见疑问解答
在使用卡诺图化简计算器的过程中,不免会有一些常见的疑问。我经常会遇到的问题之一是如何有效地选择合适的输入格式。有些工具支持多种输入方式,比如布尔表达式和真值表的输入。我在实践中发现,通过熟悉工具的输入要求,能够有效减少繁琐的调整时间。
此外,在化简结果出来后,我时常会问自己,这个结果是否是最优的?这时候有些计算器的界面会提供“验证结果”的功能。这个功能让我可以对结果进行交叉检查,确认是否存在更简化的表达形式。通过这样的功能,我能够对我的逻辑表达式化简过程有更深入的理解与把握。
经历了这些疑问与解决方案的过程,我的使用体验得到了极大改善。这不仅让我能够更顺利地使用卡诺图化简计算器,还增进了我对数字电路和逻辑表达式化简的整体理解。在这个过程中,我深刻体会到不断探索与总结的重要性。
复杂逻辑函数的化简示例
在一次课程项目中,我需要对一个复杂的逻辑函数进行化简。这一函数涉及多个输入变量,我的目标是简化为更易操作的形式。我首先将其写成布尔表达式,但尽管是经过多次尝试,依然觉得它显得过于繁琐。这时,我决定寻求卡诺图的帮助。
我输入了这个逻辑表达式,计算器快速生成了相应的卡诺图。通过图形化的方式,我能够清晰地观察到哪些区域可以合并,这让我对整个逻辑函数的结构有了更深的理解。最终,借助卡诺图的直观性,我成功地将逻辑函数化简成了一个更简单的表达式,真的感受到这种工具的强大。
应用卡诺图的步骤剖析
回想起我当时进行化简的步骤,首先是将逻辑表达式转化为真值表,这一步对于准确绘制卡诺图至关重要。接着,我在卡诺图中标注了所有真值为1的输入组合。这一过程让我意识到,准确记录每一个步骤的重要性。尤其在面对复杂函数时,任何一步的小失误都可能导致最终结果的偏差。
接下来,我连接相邻的1,寻找可能的组。通过不同的组合方式,最终我能将逻辑函数简化成最优形式。这种由简至繁的解题思路让我感受到了解契合逻辑的乐趣,也锻炼了我的逻辑思维能力。
工具与手动化简对比
在使用卡诺图化简工具后,我决定尝试手动化简相同的逻辑函数。通过对比,我发现工具能够在短时间内给出准确的结果,而手动化简则可能需要更多的时间和耐心。工具所提供的图表让我更加直观地理解了逻辑关系,而手动则需要不断进行细致的推导。
然而,手动化简让我对每一步的逻辑过程有更全面的掌握。这种对于基础原理的重视非常重要,尤其在面对更为复杂的逻辑电路时,我会感到更为自信。通过这种对比,我了解到,无论是依赖工具还是手动化简,各有优势。最理想的情况是结合两者,在快速得到结果的同时,不忘基础和原理的学习。
案例分析让我体会到了卡诺图的独特价值,它不仅是一个化简工具,同时也是一个帮助我深化理解和提升思维能力的平台。通过实践,我愈发意识到逻辑表达式化简的意义,期待在未来的学习中,继续探索这个领域的更多可能性。
智能化卡诺图化简工具的趋势
随着科技的飞速发展,智能化的卡诺图化简工具越来越受到关注。过去,我们使用卡诺图更多依赖手动操作和基本算法。如今,结合人工智能技术,在线化简工具能够分析用户输入,自动优化化简过程。这种趋势为我们提供了更高效的解决方案,尤其在处理复杂逻辑函数时,智能工具减少了人力消耗,同时提升了准确性。
我设想中的未来工具可能会结合深度学习算法,针对用户的使用习惯进行调整,提高流程的流畅度。这样的智能工具不仅可以为工程师提供便捷,更能帮助学生在学习过程中实现更深入的理解。它将无形中降低了学习曲线,让更多人能够轻松掌握逻辑电路的设计与分析。
卡诺图与其他逻辑化简方法的结合
卡诺图并不是唯一的逻辑简化方法,未来的技术发展也许会促进它与其他工具的互联互通。有可能通过与布尔代数、图论等数学理论相结合,形成更加全面的逻辑分析系统。这种综合化的工具将相对更具适应性,可以根据不同用户的需求提供多种化简方案。
我对这样的发展非常期待,想象可以通过这样的平台进行自定义设置,不论是简单的逻辑表达式还是复杂的电路设计,都能得到相应的支持。这种融合不仅能提高工作效率,还能激发创新思维,创造出更加灵活的解决方案。
在教育与工业中的应用前景
在教育领域,这些进步将改变我们教授逻辑电路设计的方式。未来,教授不再是单纯的理论传授,而是通过直观的工具与案例结合的方式,引导学生主动探索。特别是在课程设计中,能够实时看到化简前后的变化,让学生更容易理解概念,增强逻辑推理能力。
工业界同样受益匪浅。随着电子产品日益复杂,快速而准确的逻辑设计成为企业竞争的关键。在线化简工具的普及,不仅将大幅提升工程师的工作效率,还能为企业节省大量时间与成本。作为一个普通用户,我能清楚感受到这些技术变革带来的影响,相信未来的职业道路也会更轻松。
我对卡诺图化简工具的未来发展充满期待。科技和教育的交融必将推动整个领域的革新,使得学习和应用逻辑电路设计变得更加直观与高效。随着时间的推移,卡诺图的应用前景将愈加广泛,成为更多人学习和工作中不可或缺的助手。